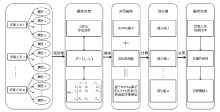
在某起电信网络诈骗案件中, 警方圈定m名涉案人员, 对每名涉案人员同时考察相同的n个证据属性, 并考虑其重要性权重的影响, 对相关属性信息进行预处理, 以语言毕达哥拉斯模糊数（linguistic Pythagorean fuzzy number, LPFN）的形式给出一系列评估信息。在此假设所有的属性都是相互独立的, 利用基于WOWA算子的软似然函数决策方法, 对得到的属性信息进行多属性研判, 从而实现对m名涉案人员的嫌疑程度结果排序, 如图1所示为本文提出的电信网络诈骗犯罪嫌疑人认定的流程示意图。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 电信网络诈骗犯罪嫌疑人认定流程图Fig.1 The flowchart of identifying suspects involved with telecom network fraud

1.2.1 语言毕达哥拉斯模糊集

专家Garg^[12]首先提出了LPFS的概念, 其定义可用简单的数学公式表示为L={(y, s_μ(y), s_v(y))|y∈Y}。其中, Y是一给定论域, S={s_ε|ε∈[0, τ]}, τ为语言术语集的基数, s_μ(y)、s_v(y)分别表示隶属度函数和非隶属度函数, LPFN表示为(s_μ(y), s_v(y)), 也可转化为简易表达式β=(s_μ, s_v), s_μ代表隶属度, s_v代表非隶属度, 满足约束条件0≤μ≤τ, 0≤v≤τ以及0≤μ²+v²≤τ²。

Garg还提出了一种比较两个LPFN的方法, 语言毕达哥拉斯模糊数β的得分值为：

$D(\beta)=\sqrt[s]{\left.\sqrt{\left(\tau^{2}+\mu^{2}\right.} v^{2}\right) / 2}$ （1）

准确值为：

$J(\beta)=\sqrt[s]{\mu^{2}+v^{2}} $ （2）

对于两个语言毕达哥拉斯模糊数β₁和β₂, 通常对两者的得分值进行较量, 有如下比较规则：

1）如果D(β₁)>D(β₂), 则β₁>β₂;

2）如果D(β₁)<D(β₂), 则β₁<β₂;

3）如果D(β₁)=D(β₂), 则比较两者准确值, 细分为以下3种情况：a. 如果J(β₁)>J(β₂), 则β₁>β₂; b. 如果J(β₁)<J(β₂), 则β₁<β₂; c. 如果J(β₁)=J(β₂), 则β₁=β₂。

1.2.2 基于WOWA算子的软似然函数方法

WOWA算子由Yager^[18]提出, 表示为一种映射：WOWA:Rⁿ→ R, 具有两个n维向量W=[w₁, ..., w_n]^T和V=[v₁, ..., v_n]^T, 其中0≤w_j≤1, ∑_jw_j=1, 且0≤v_j≤1, ∑_jv_j=1, 每个参数都与重要性权重v∈^{[0, 1]}有关, 索引函数σ _i(k)表示第k大的重要性权重, Q_i代表第i个备选方案的所有重要性权重之和, Q_ij代表第i个备选方案的前j大的重要性权重之和。

$Q_{i}=\sum_{k=1}^{n} v_{i k} $ （3）

$Q_{i j}=\sum_{k=1}^{j} v_{i \sigma_{i}(k)} $ （4）

权重值一般通过$w_{j}=f\left(\frac{j}{n}\right)-f\left(\frac{j-1}{n}\right) $公式计算 得出。

获取权重值的方法有许多, 一般引入函数f(x)=x^m(m>0)^[15], 这对于确定态度特征α极为重要, $\alpha=\int_{0}^{1} x^{m} $$d_{x}=\frac{x^{m+1}}{m+1}|1| 0=\frac{1}{m+1}$, 可以得出α∈^{[0, 1]}, α越大则代表决策者越乐观。任取态度特征α∈^{[0, 1]}, WOWA权重表示为：

$w_{i j}=\left(\frac{Q_{i j}}{Q_{i}}\right)^{\frac{1-\alpha}{\alpha}}-\left(\frac{Q_{i(j-1)}}{Q_{i}}\right)^{\frac{1-\alpha}{\alpha}} $ （5）

$\hat{w}_{i j}=\left(\frac{\left(Q_{i}-Q_{i(j-1)}\right)}{Q_{i}}\right)^{\frac{1-\alpha}{\alpha}}-\left(\frac{\left(Q_{i}-Q_{i j}\right)}{Q_{i}}\right)^{\frac{1-\alpha}{\alpha}} $ （6）

对于某备选方案A_i, 假设它在属性C_j下语言毕达哥拉斯模糊表现形式为β=(s_μ, s_v), 则传统的似然函数表示为：$L_{i}=\left(L_{i}^{\mu}, L_{i}^{v}\right)=\left(\prod_{k=1}^{j} S_{\mu_{i} \lambda_{i}(k)}, \prod_{k=1}^{j} S_{v_{i} \varphi_{i}(k)}\right) $, 基于WOWA算子的软似然函数可表示为：

$L_{i}^{W}=\left(L_{i, W}^{\mu}, L_{i, \hat{W}}^{v}\right)=\left(\sum_{j=1}^{n} w_{i j} S_{P r o d i}(j), \sum_{j=1}^{n} \hat{w}_{i j} S_{P r o d i}(j)\right)= \\ \left(\sum _ { j = 1 } ^ { n } \left(\left(\frac{Q_{i j}}{Q_{i}}\right)^{\frac{1-\alpha}{\alpha}}-\left(\frac{Q_{i(j-1)}}{Q_{i}}\right)^{\frac{1-\alpha}{\alpha}} \prod_{k=1}^{j} S_{\mu, \lambda(k)}, \right.\right. \\ \left.\sum_{j=1}^{n}\left(\left(\frac{Q_{i}-Q_{i(j-1)}}{Q_{i}}\right)^{\frac{1-\alpha}{\alpha}}-\left(\frac{Q_{i}-Q_{i j}}{Q_{i}}\right)^{\frac{1-\alpha}{\alpha}}\right)_{\prod_{k=1}^{j}} S_{v i, i(k)}\right)$ （7）

在此结合WOWA算子和软似然函数来讨论语言毕达哥拉斯模糊环境下的多属性决策方法。

步骤1：获取警方对m名涉案人员以及n个属性的评估信息, 进行预处理操作, 用LPFN的形式来表示m名涉案人员间共同的n个证据属性的评价信息LPFNs。

步骤2：引入λ_i和φ_i两个索引函数, 对LPFNs进行排序, 获得Sμ_iλ_i(k)和Sν_iφ_i(k), 并分别依次进行乘积, 得到隶属度乘积Sprod^μ_i(j)和非隶属度乘积Sprod^ν_i(j)。

步骤3：对于可疑人员A_i, 取态度特征参数α∈^{[0, 1]}, 利用公式（5）和公式（6）计算权重w_ij和Ŵ_ij, 从而利用公式（7）得出A_i隶属度和非隶属度的软似然值, 隶属度的软似然值为$\sum_{j=1}^{n} w_{i j} S_{\operatorname{Prod}_{i}^{\mu}(j)} $, 非隶属度的软似然值为$\sum_{j=1}^{n} \hat{w}_{i j} S_{\operatorname{Prod}_{i}{ }^{v}(j)}$。

步骤4：利用公式（1）计算A_i在态度特征α下的得分值D_{i, a}。

步骤5：根据得分值的大小对m名涉案人员进行排序, 得到多名涉案人员的嫌疑程度结果排序。

以浙江省某市“体育彩票”电信网络诈骗案为例。

案情概况：2021年5月1日, 报警人朱某称, 在微信群看见有人发注册体育彩票网站, 下载某飞APP后联系客服做任务赚佣金, 损失价值10万元。

受害人朱某提供了汇款的嫌疑人银行卡号, 警方在对该银行卡进行多级资金流分析研判后, 确定6名涉案银行卡的卡主, 初步认定为6名涉案人员, 即{A₁, …, A₆}, A₁=王某, A₂=李某某, A₃=周某, A₄=郑某, A₅=刘某某, A₆=吴某某。由于存在银行卡在卡主不知情时被冒名顶替的情况, 因此需要再进一步通过网络流等多属性综合决策分析, 得出这6名涉案人员的嫌疑程度结果排序。在进一步研判过程中, 警方对这6名涉案人员考虑以下五个证据属性, 即{C₁, …, C₅}, C₁=设备平台（如：微信、QQ、抖音等）的聊天内容, C₂=聊天设备IP地址和嫌疑人活动轨迹的吻合程度, C₃=涉案人员名下银行卡是否涉及其他电诈案件（串并案）, C₄=涉案人员前科情况, C₅=涉案人员经济来源情况。

在此, 我们用LPFNs来表示属性信息, 取τ=8, 具体语言术语集S如下, S={s_ε | ε=0, 1, …, τ}={非常不吻合, 很不吻合, 不吻合, 略微不吻合, 适中, 略微吻合, 吻合, 很吻合, 非常吻合}, 即：S={s₀=非常不吻合, s₁=很不吻合, s₂=不吻合, s₃=略微不吻合, s₄=适中, s₅=略微吻合, s₆=吻合, s₇=很吻合, s₈=非常吻合}。

此案例考虑了与涉案人员相关的不同属性下的重要性权重, 表1给出了评估信息。

表1

Table 1

表1(Table 1)

表1 6名涉案人员的语言毕达哥拉斯模糊信息 Table 1 Linguistic Pythagorean fuzzy information about 6 case-involved suspects 嫌疑人 C1 C2 C3 C4 C5 A1 (S7, S3), 0.5 (S6, S2), 0.4 (S3, S7), 0.3 (S2, S6), 0.8 (S5, S3), 1.0 A2 (S6, S4), 0.1 (S7, S2), 0.9 (S1, S7), 0.5 (S5, S3), 0.7 (S2, S5), 0.8 A3 (S7, S3), 0.3 (S5, S1), 0.5 (S1, S7), 0.6 (S2, S6), 1.0 (S4, S5), 0.6 A4 (S5, S2), 0.5 (S7, S3), 0.3 (S2, S7), 0.8 (S6, S1), 1.0 (S3, S4), 0.4 A5 (S7, S1), 0.8 (S6, S2), 1.0 (S3, S4), 0.5 (S1, S7), 0.3 (S5, S3), 0.4 A6 (S6, S1), 0.5 (S5, S2), 0.9 (S7, S7), 1.0 (S4, S4), 0.2 (S2, S5), 0.4

表1 6名涉案人员的语言毕达哥拉斯模糊信息 Table 1 Linguistic Pythagorean fuzzy information about 6 case-involved suspects

以态度特征α=0.2时第一名涉案人员A₁的隶属度计算为例, 来阐述基于WOWA算子的软似然函数这一多属性决策方法的应用。为验证本文方法的有效性, 采用文献^[23]中的案件算例进行对比分析。从表1能得出：

$A_{1}^{\mu}=\left\{I_{11}^{\mu}=s_{7}, I_{12}^{\mu}=s_{6}, I_{13}^{\mu}=s_{5}, I_{14}^{\mu}=s_{3}, I_{15}^{\mu}=s_{2}, \right\}$

利用公式（3）（4）（5）对重要性权重进行计算得到：

$\frac{Q_{1 j}}{Q_{1}}=\left\{\frac{Q_{11}}{Q_{1}}=\frac{1.0}{3.0}=0.3333, \frac{Q_{12}}{Q_{1}}=\frac{1.8}{3.0}=0.6, \frac{Q_{13}}{Q_{1}}=\frac{2.3}{3.0}=\right.$

$\left.0.7667, \frac{Q_{14}}{Q_{1}}=\frac{2.7}{3.0}=0.9, \frac{Q_{15}}{Q_{1}}=\frac{3.0}{3.0}=1.0\right\} $

表2为A₁的第j大隶属度的乘积$S_{P r o d_{1}^{\mu}(j)} $, 利用公式（5）和公式（7）计算权重w_j, 从而得出第一名涉案人员的隶属度的软似然值$S_{L_{1, 0.2}^{\mu}}=S_{2.8095} $, 如表3所示, 利用同样的计算方法得出其非隶属度的软似然值$S_{L_{1, 0.2}^{v}}=S_{7.4015} $。最后计算态度特征α=0.2时A₁的得分值, $D_{1, 0.2}=S_{2.9250}$。以α=0.2、α=0.5、α=0.8为例, 用同样的方法得出6名涉案人员在这三种典型态度特征值下的得分值, 如表4所示, 根据得分值D_{i, a}和准确值J_{i, a}的大小比较方法, 这6名涉案人员的嫌疑程度结果排序为A₄ >A₅ >A₆ >A₁ >A₂>A₃。

表2

Table 2

表2(Table 2)

表2 A1的第j大隶属度的乘积 Table 2 Products (correlativity) of jth weight linking to A1 有序值 $S_{\text {Prod }_{1}^{\mu}(2)}(j)$ $S_{\mu_{1} \lambda_{1}(1)}=s_{\mu_{11}}=S_{7} $ $S_{\operatorname{Prod}_{1}^{\mu}(1)}=S_{7.0000}$ $S_{\mu_{1} \lambda_{1}(2)}=s_{\mu_{12}}=s_{6}$ $S_{\text {Prod }_{1}^{\mu}(2)}=S_{7.0000} \times S_{6}=S_{5.2500} $ $S_{\mu_{1} \lambda_{1}(3)}=s_{\mu_{15}}=S_{5}$ $S_{\text {Prodí l }_{1}^{\mu}(3)}=S_{5.2500} \times S_{5}=S_{3.2813} $ $S_{\mu_{1} \lambda_{1}(4)}=S_{\mu_{13}}=S_{3}$ $S_{\text {Prod d }_{1}^{\mu}(4)}=s_{3.2813} \times S_{3}=S_{1.2305} $ $S_{\mu_{1} \lambda_{1}(5)}=S_{\mu_{14}}=S_{2} $ $S_{\text {Prod d }_{1}^{\mu}(5)}=s_{1.2305} \times S_{2}=S_{0.3076} $

表2 A1的第j大隶属度的乘积 Table 2 Products (correlativity) of jth weight linking to A1

表3

Table 3

表3(Table 3)

表3 α=0.2时A1的隶属度权重 Table 3 Correlativity and the relevant ordered weight of A1 under α=0.2 j $\left(\frac{Q_{1 j}}{Q_{1}}\right)^{4} $ $\left(\frac{Q_{1(j-1)}}{Q_{1}}\right)^{4} $ Wj $S_{\operatorname{Prod}_{1}^{\mu}(j)} $ $w_{j} s_{\text {Prodi }_{1}^{\mu}(j)} $ 1 0.0123 0.0000 0.0123 S7.0000 S1.0639 2 0.1296 0.0123 0.1173 S5.2500 S2.0229 3 0.3455 0.1296 0.2159 S3.2813 S1.5796 4 0.6561 0.3455 0.3106 S1.2305 S0.6886 5 1.0000 0.6561 0.3439 S0.3076 S0.1804 $\sum_{j} w_{j}=1 $ $\sum_{j} w_{j} S_{\operatorname{Prod}_{1}^{\mu}(j)}=S_{2.8095}$

表3 α=0.2时A1的隶属度权重 Table 3 Correlativity and the relevant ordered weight of A1 under α=0.2

表4

Table 4

表4(Table 4)

表4 WOWA下6名涉案人员的软似然值 Table 4 The soft likelihood values obtained from WOWA-operator calculation about 6 suspects 嫌疑人 α=0.2 α=0.5 α=0.8 $S_{L_{i, \alpha}^{\mu}}$ $S_{L_{i, \alpha}^{v}}$ $D_{i, \alpha} $ $S_{L_{i, \alpha}^{\mu}}$ $S_{L_{i, \alpha}^{v}} $ $D_{i, \alpha} $ $S_{L_{i, \alpha}^{\mu}} $ $S_{L_{i, \alpha}^{v}} $ $D_{i, \alpha}$ A1 S2.8095 S7.4015 S2.9250 S5.5839 S7.6020 S4.3237 S6.6603 S7.6800 S4.9688 A2 S2.7592 S7.4223 S2.8743 S5.4700 S7.5574 S4.2899 S6.6292 S7.6201 S4.9940 A3 S1.9329 S7.4240 S2.5120 S5.2766 S7.6603 S4.0720 S6.6006 S7.5124 S5.0563 A4 S2.8090 S7.2134 S3.1510 S5.5839 S7.3463 S4.5395 S6.6604 S7.4001 S5.1768 A5 S2.8058 S7.2134 S3.1496 S5.5836 S7.3462 S4.5393 S6.6603 S7.4001 S5.1768 A6 S3.1026 S7.3723 S3.1045 S5.6456 S7.5202 S4.4339 S6.6707 S7.5739 S5.0564 注：Di, a代表不同态度特征α下Ai的得分值

表4 WOWA下6名涉案人员的软似然值 Table 4 The soft likelihood values obtained from WOWA-operator calculation about 6 suspects

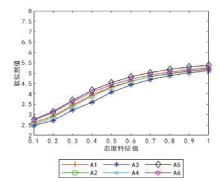
文献^[23]基于OWA算子的软似然函数方法得到的排序结果为A₄ >A₅ >A₆ >A₂ >A₁ >A₃, 图2和图3分别反映了两种方法在不同态度特征下关于6名涉案人员的软似然值, 其中纵坐标代表了得分值的下标值。可以看出, 两种方法的软似然值都随态度特征的增加而增加, 呈现了相同的趋势, 虽然两者的排序结果非常相似, 但并不完全一致, A₁与A₂之间的排序存在些许差异, 但对于嫌疑程度最大的前几名涉案人员的选择始终不变。基于WOWA算子的软似然函数能更好地减弱极值造成的影响, 并软化权重值, 使得软似然值的变化更趋于平缓, 因此, 这一比较结果可以验证所提出的基于WOWA算子的软似然函数决策方法的鲁棒性。本文充分体现了此方法的特点与优势, 不仅能够考虑到警方的态度信息, 而且可以同时兼顾各属性间的重要性权重, 为现实中普遍存在的属性权重不一致的语言模糊决策问题提供有效的解决方法。

图2

Fig.2

	Figure Option ViewDownloadNew Window
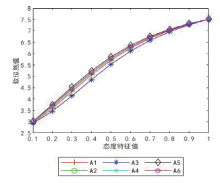	图2 不同态度特征下基于OWA算子的软似然函数值Fig.2 Soft likelihood values obtained with the OWA-operator function calcualted under different attitudinal characters

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同态度特征下基于WOWA算子的软似然函数值Fig.3 Soft likelihood values obtained with the WOWA-operator function calculated under different attitudinal characters