第一作者简介:董必强,男,江苏南京人,硕士,工程师,研究方向为痕迹检验技术。E-mail: 775738676@qq.com
针对刑侦工作中弹打玻璃类案件的侦破难点,研究一种用于计算球形弹丸抛射击打玻璃案件中弹丸飞行轨迹的算法。本文以弹丸撞击角度和撞击速度为基础参数,在阐明前置基础数据的前提下,将弹打玻璃类案件中的玻璃窗分为垂直于地面及倾斜于地面两类,采用三角函数计算和参数替换的方法,通过对弹丸撞击瞬间的弹道参数设定、弹孔图像在玻璃平面内的二维图像参数设定、相关角度的描述、计算抛物线轨迹与弹道轨迹朝向等一系列步骤,最终,研究出上述两类玻璃窗的弹道轨迹计算方法。研究表明,弹丸弹道飞行轨迹算法可以还原弹丸飞行的轨迹抛物线,作为现场弹道轨迹重建系统的核心算法使用,为开发弹打玻璃类案件的现场弹道轨迹重建系统提供了关键技术。
From time to time, such cases occur of building (usually window) glass having been broken with projectiles (bullet/pill/slug/pellet), leaving some difficult for investigators to solve. For these cases, the projectiles and their trajectories are the key clue and evidence. Therefore, this paper tries to design an algorithm to compute the ballistic trajectory of the projectile hitting towards the glass. This exploration takes the projectile’s impacting angle and velocity as basic parameters. The targeting windowpane is set under two conditions: vertical and/or tilting to the ground. Trigonometric function numeration and parameter substitution are used into calculation. Through the presetting or reverse extrapolation of several jointing parameters/factors (i.e., the ballistic parameters just at the impacting moment, the two-dimensional image parameter of bullet hole on the glass surface, the relevant angles, the parabolic track, the direction of ballistic trajectory), the ballistic trajectories are finally established about the projectile hitting glass under the two conditions. With simulation, such an algorithm of ballistic trajectory can reappear the parabolic trajectories of small spherical objects. This computation algorithm could play its role into investigating the cases with the pertinent trajectory to simulate the projectile hitting building glass.
近年来, 随着各地公安机关和公安高等院校对弹打玻璃造成的玻璃破碎痕迹的研究越来越深入, 各类研究成果不断涌现, 特别对于弹丸撞击速度和角度的研究已形成一定共识。另一方面, 随着科技水平的不断进步, 对于现场弹孔图像的测量和定位手段也越来越精准和方便。这些都为研究弹打玻璃类案件中弹丸飞行轨迹算法提供了理论支撑和技术支持。
本文结合学界已取得的成果, 在默认可以通过破碎弹孔痕迹计算弹丸撞击速度和角度的基础上研究了一套弹道轨迹计算算法, 用于还原弹丸飞行的轨迹抛物线。
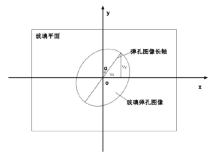
本文所研究的弹道轨迹算法是基于球形弹丸撞击玻璃遗留的玻璃破碎痕迹的二维平面形态进行计算, 对破碎痕迹的特征形态和稳定性均有一定要求。如图1所示, 本文算法所限定的弹孔图像应具备以下特征形态:1)弹孔为球形弹丸撞击玻璃形成, 弹孔痕迹呈喇叭口结构。2)弹孔弹着点痕迹清晰完整, 能反映弹丸以不同角度撞击玻璃表面时的撞击过程。
本文算法限定使用球形弹丸来进行计算, 别的不规则物体被抛射击发形成的玻璃破碎痕迹不适合本算法。在发射器具方面, 弹弓发射器发射球形弹丸击打玻璃初速大部分为100 m/s以下, 最大射击距离为200 m, 但具有高压气罐的快排发射器发射弹丸速度有可能超过200 m/s。经过初步估算, 在300 m/s以下使用抛物线计算轨迹与正常考虑阻力的差异介于5%~20%, 速度越低, 误差就会越小。而在发射弹丸均为球形弹丸且没有膛线不存在旋转因素的情况下, 各类发射器具发射金属球形弹丸的抛射击打原理相同。即气枪在一个较远距离发射弹丸与弹弓在一个较近的距离发射弹丸, 在经过不同的抛物线轨迹后撞击玻璃的瞬时动能可能相等, 撞击形成的玻璃破碎痕迹也相似[5]。所以只要玻璃破碎痕迹特征形态符合图1所示, 任何发射球形金属弹丸的发射器具均可使用本算法。由于玻璃破碎痕迹的特征需要保持稳定性, 就要求发射的球形弹丸必须具备一定的硬度和质量, 这样才能在一定的速度和撞击角度条件下形成稳定的玻璃破碎痕迹。在前期实验中, 发现金属类球形弹丸如不锈钢弹丸和钢制弹丸等形成的弹孔均符合要求, 而塑料制弹丸如BB弹等, 由于硬度和材质原因, 在撞击玻璃时易发生弹丸碎裂或者变形, 对痕迹的形成造成干扰, 无法形成稳定的特征, 故不适用本算法。在玻璃材质方面, 本算法目前是基于平板浮法玻璃进行计算, 原因是对于这类玻璃材质的弹丸撞击角度和撞击速度的研究较多, 可以提供较好的支撑, 如果将来对于钢化玻璃等其他玻璃材质的撞击理论研究有突破, 本算法可以应用于更广的范围。
弹丸被抛射击发撞击玻璃时的角度和速度数据是本文算法实施所必要的两大基础性参数。目前国内对于撞击角度的研究主要还是从撞击形成的玻璃破碎弹孔二维平面图像入手, 已取得的成果如下:1)不同角度弹丸撞击玻璃时痕迹特征形态不同的原理性分析[2]; 2)确定了玻璃破碎痕迹二维平面图像与弹丸射击角度的形态特征相关规律性[5]; 3)制定了射入口弹孔长短轴比值随射击角度变化的多项拟合公式[4]。
对于撞击速度与玻璃破碎痕迹形态的关联分析研究, 国内目前主要是从玻璃整体裂纹形态和不同发射器具的发射初速和动能比较入手, 成果如下:1)低速抛击和高速抛击的裂纹形态特征[6]; 2)不同射击器具和不同射击初速下的弹孔痕迹形态统计[1]; 3)不同材质的球形弹丸的比动能差异性研究分析[2]。
本文在弹丸撞击玻璃时的角度和速度已知的前提下, 总结了一种球形弹丸击打窗户的弹道轨迹计算方法, 此类弹丸形状固定, 在无风或微风环境中飞行受空气阻力影响较小, 速度削减为 10 % ~ 15 % 左右, 弹丸飞行弹道近似于抛物线运动轨迹, 弹道平面公式为
$\left\{\begin{array}{l}L=v_{L} \cdot t \\H=v_{H} \cdot t-\frac{1}{2} g t^{2}\end{array}\right.$
公式中的vL和vH分别为弹丸在水平和垂直方向上的分速度, 两者与弹丸飞行中的速度v存在空间几何关系, 且与v的角度数值受到以下因素影响:1)弹丸撞击玻璃的瞬时速度与玻璃平面角度; 2)弹孔痕迹在玻璃平面内的倾斜程度; 3)玻璃平面与地面的倾斜角度。
通过对弹丸撞击玻璃时的破碎痕迹的数据观察计算可以得出弹道平面与玻璃法线平面的夹角计算公式, 结合玻璃朝向方位角度的观测可以得出弹丸弹道平面的方位角。在有了方位角度数据和弹道平面计算公式后, 即可计算出弹丸在飞行时间段内的任意点三维坐标, 从而还原出整条弹道轨迹。
本文所研究的轨迹计算算法在整个弹丸弹道计算系统中位于核心地位, 需要一系列前置基础数据的支撑, 所需数据具体如下:1)弹丸撞击玻璃时的瞬时速度v。2)弹丸撞击玻璃时的瞬时角度γ 。3)弹孔痕迹在玻璃平面内的倾斜角度α 。4)弹孔所在玻璃平面与地面的角度θ 。5)弹孔所在玻璃平面的朝向方位角度δ 。6)弹孔距离地面的高度h。其中对于v和γ 的计算方法, 学界已有多篇论文研究予以支撑, 本文不再赘述; 对于α 、θ 和δ , 可以采用智能手机内置陀螺仪进行测量, 此方法操作简单精确度高, 此外也可以使用一些专用测量器具进行测量; 对于弹孔的高度, 可以采用激光测距仪进行测量。需要说明的是, 只有在以上数据都齐全的情况下算法的计算基础才成立, 本文在后续论证中均默认以上条件为已知。
本算法所针对的弹打玻璃类案件中的玻璃窗主要分为两类, 分别为:1)玻璃平面与地面垂直的窗户, 包括至少其中一种:推拉窗和平开窗。2)玻璃平面与地面呈倾斜角度的窗户, 包括至少其中一种:外开上悬窗、内开上悬窗和内开内倒窗。(见图2)
当窗户的玻璃平面垂直于地面时, 算法包括如下步骤:弹道轨迹参数计算, 取得弹丸撞击瞬间其弹道轨迹方向上的速度与玻璃平面的夹角γ 的数值; 测量弹孔图像长轴与玻璃平面y轴夹角α 的数值; 计算弹道平面与玻璃法线平面的角度β ; 计算弹道抛物线与三维坐标系中y轴角度η ; 计算弹道抛物线轨迹, 计算弹道轨迹朝向。
如图3所示, o为弹孔, v为弹丸撞击瞬间其弹道轨迹方向上的瞬时速度, x为玻璃平面的水平轴, y为玻璃平面的垂直轴, oa为v在玻璃平面的投影, 夹角γ 为v与oa之间的角度。
弹丸倾斜角度撞击玻璃时, 弹孔图像为一个椭圆形, 椭圆形长轴为弹孔图像长轴, 设弹孔图像长轴与玻璃平面y轴的夹角为α , 如图4所示, 其中弹孔图像长轴方向即为弹丸撞击瞬间其弹道轨迹方向上的速度在玻璃平面内的投影方向。
设弹丸撞击瞬间其弹道轨迹方向上的瞬时速度为v; 设弹丸撞击玻璃时有玻璃平面x轴速度vx, 玻璃平面y轴速度vy和垂直于玻璃平面的z轴速度vz; 如图3所示, 设弹道轨迹平面与平面xoz相交直线ob, 则线ob与线oz夹角即为弹道轨迹平面与玻璃法线平面yoz夹角β 。得到以下关系式:
公式1:$\sin \alpha=\frac{v_{x}}{\sqrt{v_{x}^{2}+v_{y}^{2}}}$
公式2:$\tan \gamma=\frac{v_{z}}{\sqrt{v_{x}^{2}+v_{y}^{2}}}$
公式3:$\tan \beta=\frac{v_{x}}{v_{z}}$
将上面公式1、2代入公式3:
$\therefore \tan \beta=\frac{\sin \alpha}{\tan \gamma}$
$\therefore \beta=\arctan \frac{\sin \alpha}{\tan \gamma}$
由于玻璃平面垂直于地面, 玻璃平面内x轴、y轴以及垂直于玻璃平面的z轴与地面三维坐标系中的三轴相重合。如图3所示, 弹丸撞击瞬间其弹道轨迹方向上的瞬时速度v与三维坐标系中的y轴夹角为η , ob为瞬时速度v在平面xoz上的投影, 平面yob为弹道抛物线所在平面; 如图3所示, 可得到如下关系式:
$\because\left\{\begin{array}{l}v_{y}=v_{x} \cdot \cot \alpha \\v_{x}=v_{z} \cdot \tan \beta \\v_{z}=v \cdot \sin \gamma\end{array}\right.$
$\therefore v_{y}=v \cdot \sin \gamma \cdot \tan \beta \cdot \cot \alpha$
$\because v \cdot \cos \eta=v_{y}$
$\therefore \cos \eta=\sin \gamma \cdot \tan \beta \cdot \cot \alpha$
其中, 将$\tan \beta=\frac{\sin \alpha}{\tan \gamma}, \quad \cot \alpha=\frac{\cos \alpha}{\sin \gamma}, \quad \tan \gamma=\frac{\sin \gamma}{\cos \gamma}$代入上式。
$\therefore \cos \eta=\cos \gamma \cdot \cos \alpha$
$\therefore \eta=\arccos (\cos \gamma \cdot \cos \alpha)$
由此可见, 计算夹角η 与瞬时速度v的数值无关。
将弹道抛物线轨迹平面设为横轴为弹丸轨迹飞行距离L、纵轴为弹丸轨迹飞行高度H的二维平面坐标系, 如图5所示。图中o点为弹丸撞击点即为玻璃弹孔所在位置, c点为坐标系原点, η 角为弹丸撞击瞬间其弹道轨迹方向上的瞬时速度v与y轴即H轴的夹角, a点为弹道轨迹距离地面最高点, b点为弹丸最低发射位置即地面发射位置, h为弹孔o点距离地面高度, h1为弹道轨迹最高点距离弹孔o点最大垂直距离, Lmax为弹道轨迹距离弹孔o点的最远水平距离即弹丸发射的最远距离。
根据图5可将弹道抛物线表示为以下公式:
$\left\{\begin{array}{l}L=v \cdot \sin \eta \cdot t \\H=v \cdot \cos \eta \cdot t-\frac{1}{2} g t^{2}+h\end{array}\right.$
其中, 公式中的t为时间变量。
将$\sin \eta=\sqrt{1-\cos ^{2} \eta} $、cos η =cos γ · cos α 代入可得以下公式:
$\left\{\begin{array}{l}L=v \cdot \sqrt{1-(\cos \gamma \cdot \cos \alpha)^{2}} \cdot t \\H=v \cdot \cos \gamma \cdot \cos \alpha \cdot \mathrm{t}-\frac{1}{2} g t^{2}+h\end{array}\right.$
当H=0时, 表示弹道轨迹距离弹孔o点垂直距离为-h, 即弹道轨迹已延伸至地面, 此时设定为轨迹终止。在此公式中v、γ 、α 等参数均为观测玻璃弹孔图像得到的已知量。
如图6所示, δ 为弹孔所在玻璃平面的法线的方位角, β 为弹道抛物线所在平面与玻璃平面法线所在平面的夹角, 当弹道抛物线所在平面在玻璃平面法线所在平面的右侧, 则弹道抛物线的方位角为δ +β , 当弹道抛物线所在平面在玻璃平面法线所在平面的左侧, 则弹道抛物线的方位角为δ -β , 即为弹道抛物线轨迹的朝向。
将$\beta=\arctan \frac{\sin \alpha}{\tan \gamma}$代入, 则弹道抛物线轨迹的朝向角度公式为:$\delta \pm \arctan \frac{\sin \alpha}{\tan \gamma}$。
当窗户的玻璃平面倾斜于地面时, 算法包括如下步骤:弹丸撞击瞬间其弹道轨迹方向上的瞬时速度v与玻璃平面的夹角γ 的数值; 测量弹孔图像长轴与玻璃平面y′ 轴夹角α 的数值; 测量玻璃平面与地面三维坐标系xyz中y轴之间倾角θ 的数值; 计算弹道平面与三维坐标系xyz中平面yoz的角度β ; 计算弹道抛物线轨迹, 计算弹道轨迹朝向。
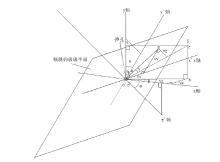
如图7所示, o′ 为弹孔, v为弹丸撞击瞬间其弹道轨迹方向上的瞬时速度, x′ 为玻璃平面的水平轴, y′ 为玻璃平面的垂直轴, z′ 为垂直于玻璃平面的法线轴, o′ a为v在玻璃平面的投影, 夹角γ 为v与o′ a之间的角度。
弹丸倾斜角度撞击玻璃时, 弹孔图像为一个椭圆形, 椭圆形长轴为弹孔图像长轴, 设弹孔图像长轴与玻璃平面y′ 轴的夹角为α , 如图7所示, 其中弹孔图像长轴方向即为弹丸撞击瞬间其弹道轨迹方向上的瞬时速度在玻璃平面内的投影方向。
设弹丸撞击瞬间其弹道轨迹方向上的瞬时速度为v; 设弹丸撞击玻璃时有玻璃平面x′ 轴速度vx′ , 玻璃平面y′ 轴速度vy′ 和垂直于玻璃平面的z′ 轴速度vz′ ; 设弹丸撞击玻璃时有地面三维坐标系xyz, 其中原点为o, o与o′ 重合, xoy平面平行于地面, yoz平面垂直于地面, 其中x轴速度vx, y轴速度vy和z轴速度vz; 如图7所示可得到以下关系式:
$ \left\{\begin{array}{l}v_{x^{\prime}}=v \cdot \cos \gamma \cdot \sin \alpha \\v_{y^{\prime}}=v \cdot \cos \gamma \cdot \cos \alpha \\v_{z^{\prime}}=v \cdot \sin \gamma\end{array}\right.$
设玻璃平面与y轴之间倾斜为θ , 其x′ 轴、y′ 轴和z′ 轴中vx′ 、vy′ 、vz′ 分解到地面三维坐标系xyz中的x轴、y轴和z轴中, 如图7所示得出下列关系式:
$\left\{\begin{array}{l}v_{x}=v_{x^{\prime}} \\v_{y}=v_{y^{\prime}} \cdot \cos \theta+v_{z^{\prime}} \cdot \sin \theta \\v_{z}=v_{y^{\prime}} \cdot \sin \theta+v_{z^{\prime}} \cdot \cos \theta\end{array}\right.$
将vx′ 、vy′ 和vz′ 的值代入上式, 可得下列关系式:
$ \left\{\begin{array}{l}v_{x}=v \cdot \cos \gamma \cdot \sin \alpha \\v_{y}=v \cdot \cos \gamma \cdot \cos \alpha \cdot \cos \theta+v \cdot \sin \gamma \cdot \sin \theta \\v_{z}=v \cdot \cos \gamma \cdot \cos \alpha \cdot \sin \theta+v \cdot \sin \gamma \cdot \cos \theta\end{array}\right.$
设弹道平面与平面yoz的夹角为β , 弹道轨迹平面与平面xoz相交直线ob, 则线ob与线oz的夹角即为弹道平面与平面yoz的夹角β 。如图7所示可得到下列关系式:
$ \tan \beta=\frac{v_{x}}{v_{z}}$
将vx和vy的值代入可得下列关系式
$ \tan \beta=\frac{v \cdot \cos \gamma \cdot \sin \alpha}{v \cdot \cos \gamma \cdot \cos \alpha \sin \theta+v \cdot \sin \gamma \cdot \cos \theta}$
$\therefore \beta=\arctan \left(\frac{\cos \gamma \cdot \sin \alpha}{\cos \gamma \cdot \cos \alpha \sin \theta+\sin \gamma \cdot \cos \theta}\right)$
如图7所示, 设弹丸撞击瞬间其弹道轨迹方向上的瞬时速度v与地面三维坐标系中的y轴夹角为η , 弹道抛物线在平面yob内, η 即为线oc与y轴的夹角;
得到下列关系式:
$ v \cdot \cos \eta=v_{y}$
将vy值代入可得下列关系式:
$\cos \eta=\cos \gamma \cdot \cos \alpha \cdot \cos \theta+\sin \gamma \cdot \sin \theta$
由此可见, 计算夹角η 与瞬时速度v的数值无关。
根据上文可将弹道抛物线表示为以下公式:
$ \left\{\begin{array}{l}L=v \cdot \sin \eta \cdot t \\H=v \cdot \cos \eta \cdot t-\frac{1}{2} g t^{2}+h\end{array}\right.$
其中, 公式中的t为时间变量, 表示不同时间下的L和H的值。
将$ \sin \eta=\sqrt{1-\cos ^{2} \eta}$, cosη =cosγ · cosα · cosθ +sinγ · sinθ 值代入可得下列关系式:
$ \left\{\begin{array}{l}L=v \cdot \sqrt{1-(\cos \gamma \cdot \cos \alpha \cdot \cos \theta+\sin \gamma \cdot \sin \theta)^{2}} \cdot t \\H=v \cdot(\cos \gamma \cdot \cos \alpha \cdot \cos \theta+\sin \gamma \cdot \sin \theta) \cdot t-\frac{1}{2} g t^{2}+h\end{array}\right.$
当H=0时, 表示弹道轨迹距离弹孔o点垂直距离为-h, 即弹道轨迹已延伸至地面, 此时设定为轨迹终止。
在此公式中v、γ 、α 、θ 等参数均为观测玻璃弹孔图像得到的已知量, t为时间变量。
根据上文所述, 可将弹道抛物线轨迹的朝向角度公式表示为:$\delta \pm \beta$, 将β 的计算式代入, 即公式为:
$ \delta \pm \arctan \left(\frac{\cos \gamma \cdot \sin \alpha}{\cos \gamma \cdot \cos \alpha \cdot \sin \theta+\sin \gamma \cdot \cos \theta}\right)$
本文所研究的弹丸弹道飞行轨迹算法, 为开发弹打玻璃类案件的现场弹道轨迹重建系统提供了可能, 可以作为系统的核心算法使用, 算法从弹丸撞击形成的玻璃破碎痕迹的二维图像入手, 采用三角函数计算和参数替换的方法, 逆向还原整条弹丸弹道轨迹, 并采用方位角计算的方法, 将计算出的弹丸弹道轨迹与实际现场环境相结合, 在获取弹孔图像所处地理坐标后, 可以运用地图引擎在核心算法的支持下还原整条弹丸弹道, 还原出发射地域。对于弹打玻璃类案件的侦办手段具有变革及突破性的意义。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|